Question

Blank/Wild: 2 tiles. O pointsA: 9 tiles, 1 pointB: 2 tiles, 3 pointsC: 2 tiles, 3 pointsD: 4 tiles, 2 pointsE: 12 tiles, 1 pointF: 2 tiles, 4 pointsG: 3 tiles, 2 pointsH: 2 tiles, 4 pointsI: 9 tiles, 1 pointJ: 1 tile, 8 pointsK: 1 tile, 5 pointsL: 4 tiles, 1 pointM: 2 tiles. 3 pointsN: 6 tiles. 1 pointO: 8 tiles 1 pointP: 2 tiles, 3 pointsQ: 1 tile, 10 pointsR: 6 tiles, 1 pointS: 4 tiles, 1 pointT: 6 tiles, 1 pointU: 4 tiles, 1 pointV: 2 tiles, 4 pointsW: 2 tiles. 4 pointsX: 1 tile, 8 pointsY: 2 tiles, 4 pointsZ: 1 tile, 10 points4. Above is a graphic showing the distribution of tiles in Scrabble, showing how many of eachletter there are as well as how many points there are worth. Note that there are 100 tilestotal.(a) What is the probability of picking a tile worth one point?(3 points)

Answer 1

Answer: 0.68

First, we list down all the letters that represent 1 point.

We have:

A: 9 tiles

E: 12 tiles

I: 9 tiles

L: 4 tiles

N: 6 tiles

O: 8 tiles

R: 6 tiles

S: 4 tiles

T: 6 tiles

U: 4 tiles

Then, we will get the total number of these tiles:

`9+12+9+4+6+8+6+4+6+4=68`

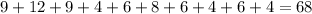
Next, since there are 100 tiles in total, we will divide the number of tiles worth 1 point by 100:

`\begin{gathered} P=\frac{\text{ number of tiles worth 1 point }}{\text{ total number of tiles }} \\ P=(68)/(100) \\ P=(17)/(25)=0.68=68\% \end{gathered}`

Therefore, the probability of picking a tile worth 1 point is 0.68.