Question

Find the equation of the line that passes through the x-intercept of the line 5x - 7y + 45 = 0 and is perpendicular to the line y = 25x - 3.

Answer 1

To get the x-intercept of the line 5x - 7y + 45 = 0, we need to assume that the value of y = 0. With that, we have:

`\begin{gathered} 5x-7y+45=0 \\ 5x-7(0)+45=0 \\ 5x=-45 \\ (5x)/(5)=-(45)/(5) \\ x=-9 \end{gathered}`

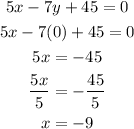
Therefore, the x-intercept of this line is at (-9, 0).

A line perpendicular to the line y = 25x - 3 must have a slope that is negative reciprocal to the slope of line y = 25x - 3. Since the slope of this line is 25, therefore the line perpendicular to it must have a slope of -1/25.

Now, we have a point at (-9, 0) and a slope of -1/25. Let's determine its equation using the point-slope form formula below.

`\begin{gathered} y-y_1=m(x-x_1) \\ y-0=(-1)/(25)(x+9) \\ 25y=-x-9 \\ 25y+x=-9 \end{gathered}`

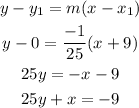
Therefore, the equation of the line that passes through the x-intercept of the line 5x - 7y + 45 = 0 and is perpendicular to the line y = 25x - 3 is 25y + x = -9 or 25 + x + 9 = 0.