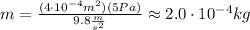Question

A cube of an unknown mass is placed on a flat surface. The cube has a volume of 8 cm^3. If the pressure exerted by the cube on the surface is 5 Pa, what must be the mass of the cube?

Answer 1

First, take into account that the pressure exerted by a force on a certain area, is given by:

`P=(F)/(A)`

In this case, the force F is the weight of the box, that is:

F = W = m*g

where m is the mass of the box and g the acceleration gravitational constant 9.8m/s^2.

The area where the force due to the weight is applied is given by:

`A=a^2`

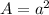
where a is the length of the side of the box. To find the value of a, you can use the information about the volume of the box, as follow:

`\begin{gathered} V=a^3 \\ a=\sqrt[3]{V} \\ a=\sqrt[3]{8cm^3} \\ a=2cm \end{gathered}`

Now, you can calculate the area A (but in this case we express a in meters by convenience):

`\begin{gathered} a=0.02m \\ A=(0.02m)^2=4\cdot10^(-4)m^2 \end{gathered}`

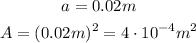
Next, in the expression for the pressure P=F/A, replace F by m*g and solve for m:

`\begin{gathered} P=(m\cdot g)/(A) \\ m=(A\cdot P)/(g) \end{gathered}`

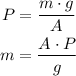
All parameters A, P and g are known parameters, then, you obtain:

`m=((4\cdot10^(-4)m^2)(5Pa))/(9.8(m)/(s^2))\approx2.0\cdot10^(-4)kg`