Question

“A vine called the mile-a-minute weed is known for growing at a very fast rate. It can grow up to .5 ft per day. How fast in inches per hour can the mile-a-minute weed grow up to? Show your work using the correct conversion factors.”

Answer 1

`a)\text{rate}=2.5\frac{\text{ inches}}{\text{hour}}`

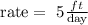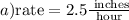
Step-by-step explanation

to solve this we need to convert measure units, so we can use equivalent fractions:

to do that, it is necesarry to know the equivalences

`\begin{gathered} 1\text{ ft= 12 inches} \\ 1\text{ mi= 5280 ft} \\ 1\text{ day= 24 hours} \\ 60\text{ minutes = 1 hour} \end{gathered}`

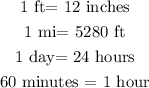
when multiplying by a equivalent fraction, the amount is not affected, just the unit of measure, so

so

a)

Let

`\text{rate}=\text{ 5}\frac{ft}{\text{day}}`

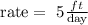
now, convert ( multiply by the favourable equivalent fraction)

`\begin{gathered} \text{rate}=\text{ 5}\frac{ft}{\text{day}}(\frac{1\text{ day}}{24\text{ hours}})(\frac{12\text{ inches}}{1\text{ ft}}) \\ \text{rate}=\text{ 5}\frac{ft}{\text{day}}(\frac{1\text{ day}}{24\text{ hours}})(\frac{12\text{ inches}}{1\text{ ft}})=2.5\frac{\text{ inches}}{\text{hour}} \\ \text{rate}=2.5\frac{\text{ inches}}{\text{hour}} \end{gathered}`

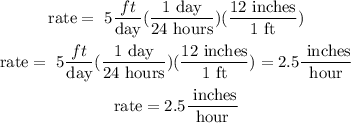
b) now, in miles per minute

so

`\text{rate}=\text{ 5}\frac{ft}{\text{day}}`