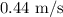Given:
The mass of the bean is
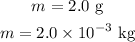
The distance during which it traveled is
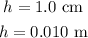
Required: (a) Potential energy gained
(b) the speed of the bean when lands back in the palm.
Explanation:
we have to apply conservation of energy to solve the problem.
when the bean is in our hand it has zero potential energy and after reaching its highest point has only potential energy.
look at the free body diagram
The potential energy is given as
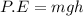
here,

is the height and
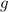
is the acceleration due to gravity which is equal to
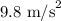
Plugging all the values in the above relation, we get
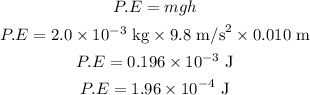
(a) Potential energy is

(b)
By energy conservation,
when a bean comes down in the hand, total potential energy is converted into kinetic energy.
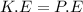
Kinetic energy is given as
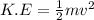
put this into the above relation, we get
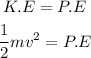
![v=\sqrt[2]{2*(P.E)/(m)}](https://img.qammunity.org/2023/formulas/physics/college/h408nt0u5hy3dj7nmtwqa3xapk8q5bjfvq.png)
Plugging all the values in the above relation, we get
![\begin{gathered} v=\sqrt[2]{2*1.96*\frac{10^{-\frac{4}{}}\text{ J}}{2*10^(-3)\text{ kg}}} \\ \\ v=\sqrt[2]{1.96*10^(-1)} \\ v=0.44\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/1a761kjg6k8k3vskfefwyaitiafsaqd4ci.png)
Thus, the speed of the bean as lands back in the palm is