We want to solve the following equation
![\frac{2-i\sqrt[]{3}}{2+i\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/jsk3tydjwptjnp61pm7rh6fuygyn077tcr.png)
Where i is the imaginary number.
Using the following property
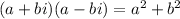
We can rewrite our equation by multiplying both numerator and denominator by the denominator complex conjugate.
![\frac{2-i\sqrt[]{3}}{2+i\sqrt[]{3}}=\frac{(2-i\sqrt[]{3})\cdot(2-i\sqrt[]{3})}{(2+i\sqrt[]{3)}\cdot(2-i\sqrt[]{3})}](https://img.qammunity.org/2023/formulas/mathematics/college/jnm3bhn05l7pvbn15lcp3r4yuxu1ux9irl.png)
Expanding those products, we have
![\begin{gathered} \frac{(2-i\sqrt[]{3})\cdot(2-i\sqrt[]{3})}{(2+i\sqrt[]{3)}\cdot(2-i\sqrt[]{3})}=\frac{(2-i\sqrt[]{3})\cdot(2-i\sqrt[]{3})}{2^2+(\sqrt[]{3})^2} \\ =\frac{4-2i\sqrt[]{3}-2i\sqrt[]{3}-3}{4+3^{}} \\ =\frac{1-4i\sqrt[]{3}}{7^{}} \\ =(1)/(7)-\frac{4\sqrt[]{3}}{7^{}}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/olvgptkkyz04id49ue60g51uwfyxx481s0.png)
And this is the solution for our problem.
![(1)/(7)-\frac{4\sqrt[]{3}}{7^{}}i](https://img.qammunity.org/2023/formulas/mathematics/college/mbysad4elxjyn0t7jbbyb0pi16npu7cisc.png)