We are given the following sequence
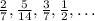
Let us check if there is a common difference between the consecutive terms

As you can see, there is a common difference between the terms that is 1/14
If we add 1/14 to the last term of the sequence (1/2) then we would get the next fraction in the sequence.
![undefined]()