Question

Suppose a random variable, x, arises from a binomial experiment. Suppose n = 10, and p = 0.81. a. Write the probability distributionb. Draw a histogramc. Describe the shape of the histogramd. Find the meane. Find the variablef. Find the standard deviation

Answer 1

Given a random variable, x that arises from a binomial experiment and suppose that n = 10, and p = 0.81.

PART A:

The probability distribution for a binomial experiment is given as

`\begin{gathered} b\mleft(x;n,p\mright)=^nC_xp^(x()(1-p)^(n-x) \\ b(x;n,p)=^nC_xp^(x()(q)^(n-x) \\ b(x;n,p)=^(10)C_x(0.81^x)(0.19)^(10-x) \end{gathered}`

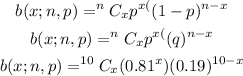
where q =1-p

PART B

One way to illustrate the binomial distribution is with a histogram. A histogram shows the possible values of a probability distribution as a series of vertical bars. The height of each bar reflects the probability of each value occurring.

The histogram is given below:

PART C

The shape of the histogram shows it is skewed to the left.

PART D.

The mean of a binomial experiment is given below:

`\begin{gathered} \mu=n* p \\ \mu=10*0.81 \\ \mu=8.1 \end{gathered}`

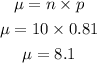
PART E

The variance of a binomial experiment is

`\begin{gathered} \text{Variance= n x p x q} \\ =10*0.81*0.19 \\ =1.539 \end{gathered}`

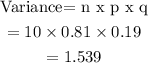
PART F

The standard deviation is the square root of the variance.

`\begin{gathered} sd=\sqrt[]{\text{variance}} \\ sd=\sqrt[]{1.539} \\ s\mathrm{}d=1.241 \end{gathered}`