Question

How many pounds of candy that sells for $4.25 per Ib must be mixed with candy that sells for $2.75 per Ib to obtain 10 lb of a mixture that should sell for $3.95 per Ib?

Answer 1

Given:

There are given that candy that sells for $4.25 per lb that mixed with candy that sells for $2.75 per lb.

Step-by-step explanation:

Let pounds of candy be x = 4.25 and mixed candy be y = 2.75.

Then,

We need to set the equations:

So,

`\begin{gathered} x+y=10...(1) \\ 4.25x+2.75y=3.95*10 \\ 4.25x+2.75y=39.5\text{ ....\lparen2\rparen} \end{gathered}`

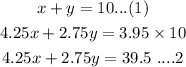
Now,

Multiply 2.75 with the equation (1) and subtract equation (1) from equation (2):

So,

`\begin{gathered} (x+y=10)*2.75 \\ 2.75x+2.75y=27.5 \end{gathered}`

Then,

Subtract equation (1) from the equation (2):

So,

`\begin{gathered} (4.25-2.75)x=39.5-27.5 \\ 1.5x=12 \\ x=(12)/(1.5) \\ x=8 \end{gathered}`

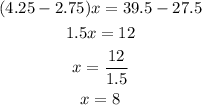
Final answer:

Hence, the answer is 8 lb.