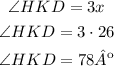5)
For the figure, lines AB and CD are crossed by a transversal line FE.
If lines AB || CD, then the angles, ∠BHK, and ∠HKD are supplementary angles, which means they add up to 180º.
So we can say that:
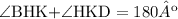
We know that
∠BHK= (2x+50)º
∠HKD= (3x)º
Replace both measures in the expression above and you can determine an equation with "x" as the only unknown

Order the like terms together and simplify
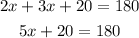
Now you can determine the value of x. First, pass 50 to the other side of the equal sign by applying the opposite operation to both sides of it:
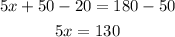
Second, divide both sides of the expression by 5 to reach the value of x:
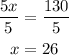
Once determined the value of x, you can calculate the measures of the angles ∠BHK and ∠HKD
6)
7)