Answer:
100 moles of oxygen
Explanations:
Given the chemical reaction between the hydrocarbon compound and oxygen expressed as:

Based on stoichiometry, you can see that 2 moles of the hydrocarbon compound react with 25 moles of oxygen. Therefore if 8 moles of the hydrocarbon in the equation fully react, the number of moles of oxygen needed will be expressed as:
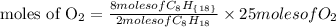
The number of moles of oxygen needed will be simplified further as:
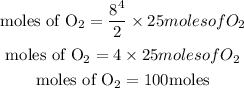
This shows that if 8 moles of the hydrocarbon in the equation fully react, 100 moles of oxygen would be needed.