Step-by-step explanation
Algebra / Linear Equations / Linear Equations in the Real World / Applications Using Linear Models
From the statement, we know that:
• there are initially y₀ = 30 weeds in a yard,
,
• each day 5 more weeds appear, so the rate of change is m = 5 weeds/day.
a) Defining the variable x for the number of days, and y for the number of weeds, we have:
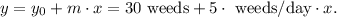
Or simply we can write:
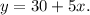
b) We want to know how many days (x) we need to have y = 100 weeds in the yard. So we must solve for x the equation:
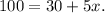
Solving for x, we get:
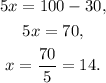
Answer
a) The equation to model the situation is:
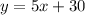
b) We need 14 days to reach 100 weeds in the yard.