Question

I will provide another picture with the questions for this problem provided Please, note that this lengthy. And “complex” if you will, and the subject is pre calculus.

Answer 1

• Albert's balance =$2159.07

,

• Marie's balance = $2244.99

,

• Han's balance = $2188.35.

,

• Max's balance = $2147.36

,

• Marie

Step-by-step explanation:

The compounded interest formula for an amount (Ao) compounded k times in a year over a period of t years at r% per annum is:

`A(t)=A_o(1+(r)/(k))^(kt)`

For continous compounding, we make use of the formula:

`A(t)=A_oe^(rt)`

Albert

$1000 earned 1.2% annual interest compounded monthly

`A(10)=1000(1+(1.2)/(12*100))^(12*10)=\$1127.43`

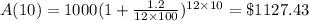
$500 lost 2% over the course of the 10 years

`A(10)=500(1-(2)/(100))=500*0.98=\$490`

$500 grew compounded continuously at rate of $0.8% annually.

`A(10)=500* e^(0.008*10)=\$541.64`

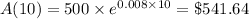
Albert's balance after 10 years will be: 1127.43+490+541.64=$2159.07

Marie

$1500 earned 1.4% annual interest compounded quarterly.

`A(10)=1500(1+(1.4)/(4*100))^(4*10)=\$1724.99`

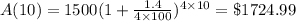
$500 gained 4% over the course of 10 years

`A(10)=500(1+(4)/(100))=500*1.04=\$520`

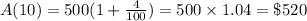
Marie's balance after 10 years will be: 724.99+520=$2244.99

Hans

$2000 grew compounded continuously at rate of 0.9% annually.

`A(10)=2000* e^{(0.9)/(100)*10}=\$2188.35`

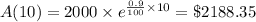
Han's balance after 10 years will be $2188.35.

Max

$1000 decreased in value exponentially at a rate of 0.5% annually.

`A(10)=1000(1-0.5\%)^(10)=1000*0.995^(10)=\$951.11`

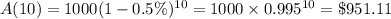
$1000 earned 1.8% annual interest compounded biannually (twice a year).

`A(10)=1000(1+(1.8)/(2*100))^(2*10)=\$1196.25`

Max's balance after 10 years will be 951.11+1196.25=$2147.36

Therefore, after 10 years:

• Albert's balance =$2159.07

,

• Marie's balance = $2244.99

,

• Han's balance = $2188.35.

,

• Max's balance = $2147.36

Since Marie's balance is the highest, she is $10,000 richer.