Question

An object has an acceleration of 6.0 m/s/s. If the net forcewas tripled and the mass were doubled, then the newacceleration would be m/s/s.

Answer 1

We are given that an object has an acceleration of 6 m/s^2. According to Newton's second law we have that the force is the product of the mass by the acceleration:

`F=ma`

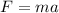
Where:

`\begin{gathered} F=\text{ force} \\ m=\text{ mass} \end{gathered}`

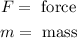
We can solve for the acceleration by dividing both sides by the mass:

`(F)/(m)=a`

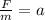
Since the original acceleration is 6 m/s^2 we have:

`(F)/(m)=6(m)/(s^2)`

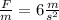
Now, for the new acceleration, we are given that the new force is 3 times the original force and the mass is double the original mass, therefore, we can substitute:

`(3F)/(2m)=a`

But, we already established that:

`(F)/(m)=6`

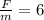
Therefore:

`(3)/(2)(6(m)/(s^2))=a`

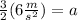
Therefore, solving the operations, the new acceleration is:

`9(m)/(s^2)=a`

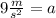
Therefore, the acceleration is 9 meters per second squared.