Question

2) Find the measure of all three angles in the tollowing triangles: a) 2x L Xriso B 3x-450 С C b) Right Triangle hy Fy-220

Answer 1

Solving Problems on Angles of a Triangle.

The sum of all the three angles in a triangle is 180 degrees, hence:

a.

`\begin{gathered} \angle A\text{ +}\angle B\text{ + }\angle C=180^o \\ 2x\text{ + (3x-45) + (x + 15) =180} \\ \text{Clear the bracket.} \\ 2x+3x-45+x+15=180 \\ \text{Collecting like terms, we get} \\ 2x+3x+x=180+45-15 \\ 6x=225-15 \\ 6x=210 \\ \text{Dividing both sides by 6, we get} \\ x=(210)/(6)=35 \end{gathered}`

So, the angles of the triangles are;

angle A = 2x = 2(35) = 70 degrees.

angle B = 3x - 45 = 3(35) - 45 = 105 - 45 = 60 degrees.

angle C = x+15 = 35 + 15 = 50 degrees.

The correct answers are 70 degrees, 60 degrees, and 50 degrees.

b.

`\begin{gathered} \angle A\text{ + }\angle B\text{ + }\angle C\text{ = 180 }\ldots(\text{angle sum of a triangle)} \\ 4y+3y-22\text{ +90 = 180} \\ \text{Collecting like terms, we get} \\ 7y\text{ + 68 = 180} \\ 7y\text{ =180 -68} \\ 7y\text{ = 112} \\ \text{Dividing both sides by 7, we get} \\ y=(112)/(7)=16 \end{gathered}`

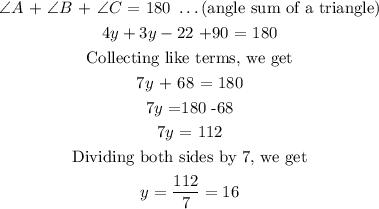
Thus, the angles are;

angle A = 4y = 4(16) = 64 degrees

angle B = 3y - 22 = 3(16) - 22 = 48 - 22 = 26 degrees

angle C = 90 degrees

The correct answer are 64 degrees , 26 degrees , and 90 degrees.