Question

The graph of f(x)= (1.68)^x is reflected about the x axis and shifted upward 7 units. When submitting non-integer answers use a decimal (not fraction) and round to the nearest hundredth.The coefficient on our transformed function is AnswerThe exponent on our transformed function is AnswerThe y intercept on our transformed function is Answer The domain on our transformed function is Answer The range on our transformed function is Answer

Answer 1

`f(x)=(1.68)^x`

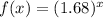
A reflection about the x-axis means that we have to flip the function over the horizontal axis (x-axis). In order to do so, we have to add a negative sign outside the coefficient of the function as follows:

`f(x)=-(1.68)^x`

We have a negative sign outside the parenthesis, thus the coefficient of the transformed function is still 1.68.

As we did not change the exponent, then the exponent is still x.

Finally, as the problem is asking to shift the function upward 7 units, then we have to add this to our transformed function:

`f(x)=-(1.68)^x+7`

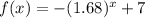
In the graph above, we can see how our original function (red line) made a reflection about the x-axis (blue line), and finally shifted 7 units (purple line).

To calculate the y axis we have to set x to 0:

`f(0)=-(1.68)^0+7`

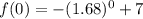
Simplifying:

`f(x)=-1^{}+7=6`

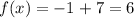
The y-intercept of the transformed function is (0, 6), as it is also seen in the graph.

Finally, the domain includes all real numbers, while the range includes all real numbers less than 7.

Answer:

`f(x)=-(1.68)^x+7`

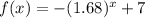
• Coefficient: 1.68

,

• Exponent: ,x

,

• y-intercept: ,(0, 6)

,

• Domain: all real numbers.

,

• Range: all real numbers less than 7