Question

Michael bought 4½ pounds of soil. He used 1⅔ pounds of soil in a pot for his tomatoes and used ¼ pound of soil in a pot for his basil plant. After planting his tomatoes and basil, how many pounds of soil did Michael have left?

Answer 1

Fractions

We need to do some operations with fractions, concretely adding and subtracting fractions.

Michael had 4½ pounds of soil. First of all, we need to express this compound number into a single fraction. Then we write:

`4(1)/(2)=4+(1)/(2)`

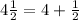
To add these two numbers we need that both have the same denominator. One easy way to do that is to multiply 4*2=8 and then write:

`4+(1)/(2)=(8)/(2)+(1)/(2)=(9)/(2)`

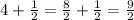
Once the denominators are equal, we just simply add the numerators.

Now convert the next compound number to a single fraction:

`1(2)/(3)=1+(2)/(3)`

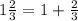
Again, we multiply the whole number by the denominator 1*3 =3 and write:

`1+(2)/(3)=(3)/(3)+(2)/(3)=(5)/(3)`

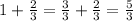
Now we get into the logic of the problem. To find how many pounds of soil were left, we need to subtract the pounds used for the tomatoes and the pounds used for the basil plant. The calculations are:

`(9)/(2)-(5)/(3)-(1)/(4)`

This time we need to find the LCM of the three denominators. We write all three of them as the product of their prime factors:

2 = 2

3 = 3

4 = 2*2

We select the prime numbers with their highest exponent:

LCM = 2*2*3 = 12

Now divide 12 by each denominator and multiply by each numerator:

`(9\cdot6-5\cdot4-1\cdot3)/(12)`

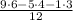
Calculating:

`(54-20-3)/(12)=(31)/(12)`

Michael had 31/12 pounds of soil left