Given the functions:

You need to multiply them in order to find:

Then, you need to set up:
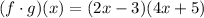
In order to multiply the binomials, you can use the FOIL Method, which states that:
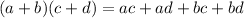
You also need to remember the Sign Rules for Multiplication:

Then, you get:
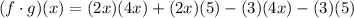
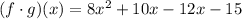
Now you have to add the like terms (these are the terms that have the same variables with the same exponents):

Hence, the answer is: Option D.