Solution:
This is a question on word problem.
We develop each statement into mathematical expressions.
Let the following letters represent the calls received for three evenings
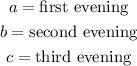
The statements are written as equations below;

Substituting equations (3) and (2) in equation (1);
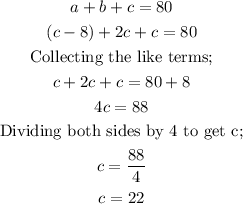
Substituting the value of c in equations (2) and (3) to get b and a respectively,
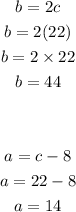
Therefore,
First evening = 14 phone calls
Second evening = 44 phone calls
Third evening = 22 phone calls