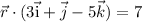Question

Determine the vector equation of the plane with the cartesian equation 3x+y-5z-7=0.

Answer 1

Given

The cartesian equation of a plane is 3x+y-5z-7=0.

To determine the vector equation of the plane.

Step-by-step explanation:

It is given that,

The cartesian equation of a plane is 3x+y-5z-7=0.

That implies,

`3x+y-5z=7`

Since the general equation of a plane is

`\vec{r}\cdot\hat{n}=d`

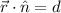
From, the cartesian equation, d=7.

Then,

`\begin{gathered} (x\vec{i}+y\vec{j}+z\vec{k})\cdot\hat{n}=7 \\ \because3x+y-5z=7 \\ Then, \\ (x\vec{\imaginaryI}+y\vec{j}+z\vec{k})\hat{\cdot n}=3x+y-5z \\ \therefore\hat{n}=3\vec{\mathrm{i}}+\vec{j}-5\vec{k} \end{gathered}`

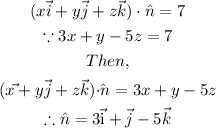
Hence, the vector equation is,

`\vec{r}\cdot(3\vec{\mathrm{i}}+\vec{j}-5\vec{k})=7`