Question

11. Try this.... remember you have been adding, subtracting or multiplyingpolynomials for this entire assignment...You have a rectangle with length (x+3) and width (2x+5). What is the....a) perimeter of the rectangleb) area of the rectangle

Answer 1

The perimeter and area of a rectangle are calculated as:

`\begin{gathered} \text{ Perimeter = 2(length) + 2(width)} \\ \text{ Area = (length})\cdot(\text{width)} \end{gathered}`

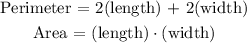
Now, we can calculate the perimeter of the rectangle as follows:

`\text{Perimeter = 2(x+3) + 2(2x+5)}`

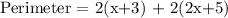
Applying the distributive property and adding like terms, we get:

`\begin{gathered} \text{Perimeter = (2}\cdot x)+(2\cdot3)+(2\cdot2x)+(2\cdot5) \\ \text{Perimeter = 2x + 6 + 4x + 10} \\ \text{Perimeter = 6x + 16} \end{gathered}`

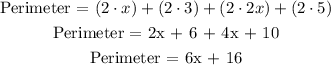
At the same way, the area is equal to:

`\begin{gathered} \text{Area = (x+3)(2x+5)} \\ \text{Area = (x}\cdot2x)+(x\cdot5)+(3\cdot2x)+(3\cdot5) \\ \text{Area = 2x}^2+5x+6x+15 \\ \text{Area = 2x}^2+11x+15 \end{gathered}`

Answers: Perimeter = 6x + 16

Area = 2x² + 11x + 15