Question

Find the vertex by substituting the value of x into the quadratic equation.

Answer 1

Vertex = (1, 1)

Explanation:

Given the quadratic equation:

`y-x^2+2x=2`

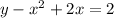
First, rewrite the equation in the standard form y=ax²+bx+c:

`\begin{gathered} y=x^2-2x+2 \\ \implies a=1,b=-2,c=2 \end{gathered}`

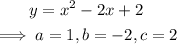
The value of x at the vertex is obtained using the formula for the equation of symmetry below:

`\begin{gathered} x=-(b)/(2a) \\ x=-(-2)/(2*1)=1 \end{gathered}`

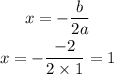
Next, substitute x=1 into the quadratic function:

`\begin{gathered} y=x^2-2x+2 \\ =1^2-2(1)+2 \\ y=1 \end{gathered}`

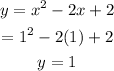
The vertex of the quadratic function is (x, y) = (1, 1).

The first option is correct.