Question

9 ft19 ftPlease refer to the rounding rules in the instructions.Circumference of the base =feetArea of the base =square feetSlant height =feetHeight =feetLateral area =square feetSurface area =square feetVolume =cubic feetBlank 1:Blank 2:Blank 3:Blank 4:Blank 5:Blank 6:Blank 7:

Answer 1

First, we can find the circumference using the following equation, given that the radius of the base is 9 ft:

`\begin{gathered} C=2\pi r=2(3.14)(9)=56.52ft \\ \Rightarrow C=56.52ft \end{gathered}`

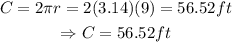
we have that the circumference of the base is 56.52ft

2.- Next,we can find the area of the base using the formula for the area of a circle:

`\begin{gathered} A=\pi r^2=(3.14)(9)^2=254.34ft^2 \\ \Rightarrow A=254.34ft^2 \end{gathered}`

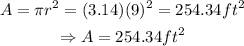
then, the area is 254.34ft^2.

3.The slant height is given, and its value is 19 ft

4.-We can find the height using the radius and the slant height with the pythagorean theorem:

`\begin{gathered} h=\sqrt[]{(19)^2-(9)^2}=\sqrt[]{361-81}=\sqrt[]{280}=2\sqrt[]{70} \\ \Rightarrow h=2\sqrt[]{70}=16.73 \end{gathered}`

thus, the height is 2*sqrt(70) = =16.73ft

5.-The lateral area of the cone can be found using the following equation:

`\begin{gathered} L=\pi r\cdot\sqrt[]{r^2+h^2}=(3.14)(9)\cdot\sqrt[]{(9)^2+(16.73)^2}=536.86ft^2 \\ \Rightarrow L=536.86.ft^2 \end{gathered}`

6.- We have the following general rule for the surface area:

`\begin{gathered} A_c=\text{lateral surface area + base area} \\ =536.86+254.34=791.2ft^2 \\ \Rightarrow A_c=791.2ft^2 \end{gathered}`

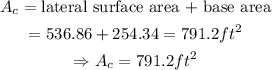
thus, the surface area of the cone is 791.2ft^2

7.-Finally, for the volume of the cone, we have:

`\begin{gathered} V=(1)/(3)\pi r^2h=(1)/(3)(3.14)(9)^2(16.73)=1418.37ft^3 \\ \Rightarrow V=1418.37ft^3 \end{gathered}`

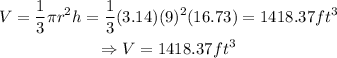
therefore, the volume of the cone is 1418.37ft^3