Question

BCDE is a rhombus. Find the missing measures.BC = 28 and BD = 32CD =FD =EF =EC =

Answer 1

We know that diagonals bisect each other perpendicularly, so we can draw the following picture:

Then, from the right triangle FED,

we have that

`x^2+16^2=28^2`

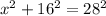
which gives

`x^2=784-256`

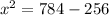
then

`\begin{gathered} x^2=528 \\ x=\sqrt[]{528} \\ x=\sqrt[]{16\cdot33} \\ x=4\sqrt[]{33} \end{gathered}`

Therefore,

`EF=x=4\sqrt[]{33}`

Since EC is twice EF, then

`EC=8\sqrt[]{33}`

Finally, we know that all sides are equal, this means that

`BC=ED=28=CD=BE`

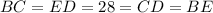
In summary, the answers are:

`\begin{gathered} CD=28 \\ FD=(32)/(2)=16 \\ EF=4\sqrt[]{33} \\ EC=8\sqrt[]{33} \end{gathered}`