Given data:
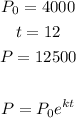
Use the given data in the model and solve k (growth rate):
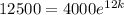
Divide both sides of the equation into 4000:
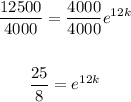
Find the natural logarithm of both sides of the equation:
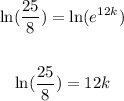
Divide both sides of the equation by 12:
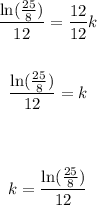
Evaluate:
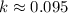
Then, the growth rate is 0.095 (9.5%)