Question

A silver dollar is dropped 960 feet from the top floor of a hotel at time T=0. The position as a function of time for this object is S (t)= -16t^2+960. A) find the average rate of change for 1≤t≤4.B) find the instantaneous rate of change at t=3C) how long will it take for the dollar to hit the ground ?D) find the instantaneous rate of change of the dollar just before it hits the ground?

Answer 1

Equation: S (t)= -16t^2+960

A) The average rate of change of a function over an interval (a,b) is given by:

`avarege\text{ rate of change = }\frac{change\text{ in y}}{change\text{ in x}}=(s(b)-s(a))/(b-a)`

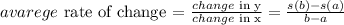
Then:

`average\text{ rate of change = }(s(4)-s(1))/(4-1)`

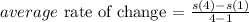
For s(4)

`s(4)=-16(4)^2+960=-16(16)+960=-256+960=704`

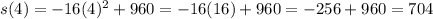
For s(1)

`s(1)=-16(1)^2+960=-16+960=944`

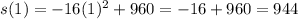
Therefore average rate of change is:

`(704-944)/(4-1)=(-240)/(3)=-80`

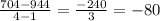
Answer: average rate of change = - 80 ft/s

B) This is just the value of the derivative when t = 3, so

`\begin{gathered} s(t)=-16t^2+960 \\ s^(\prime)(t)=-2(16)t^(2-1)+0=-32t \\ s(3)=-32(3)=-96 \end{gathered}`

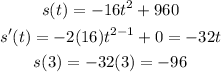
Answer: the instantaneous rate of change = - 96 ft/s

C) This is when s = 0, so:

`\begin{gathered} -16t^2+960=0 \\ -16t^2+960-960=0-960 \\ -16t^2=-960 \\ (-16t^2)/(-16)=(-960)/(-16) \\ t^2=60 \\ t=\sqrt[]{60} \\ t=7.75 \end{gathered}`

Answer: time = 7.75 s

D) This happens when t = 7.75, so:

`s^(\prime)(7.75)=-32(7.75)=-248`

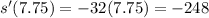
Answer: instantaneous rate of change of the dollar just before it hits the ground = - 248 ft/s