Question

A theater has 32 rows of seats. If there are 26 seats in the 1st row, 30 in the 2nd, 34 in the 3rd, and so on, how many seats are there in all? Assume the pattern continues.

Answer 1

Arithmetic Sequences

It's a sequence of terms that follow the following pattern: Each term is obtained by adding a constant number to the previous term. That constant number is called the common difference.

The formula to calculate the nth term is:

`a_n=a_1+(n-1)\cdot d`

Where a1 is the first term, d is the common difference, and n is the number of the term.

The sum of the n first terms of an arithmetic sequence is:

`S_n=(a_1+a_n)/(2)\cdot n`

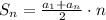
A theater has 32 rows of seats. In the first row, there are 26 seats. In the second row, there are 30 seats, 34 in the 3rd, and so on. This produces the following arithmetic sequence:

26, 30, 34, ....

The common difference is calculated by subtracting two consecutive terms:

d = 30 - 26 = 4

The number of seats for the 32nd row is:

`\begin{gathered} a_(32)=26+(32-1)\cdot4 \\ a_(32)=26+124=150 \end{gathered}`

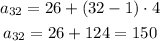
The total of seats in the theater is:

`\begin{gathered} S_(32)=(26+150)/(2)\cdot32 \\ S_(32)=(176)/(2)\cdot32 \\ S_(32)=2816 \end{gathered}`

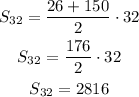
There are 2816 seats in the theater