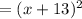Given the expression written in the following form:
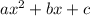
You can complete the square for the expression by following these steps:
1. You must take the coefficient "b", divide it by 2 and then you must square it:
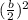
For this case you can identify that "b" is:
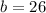
Therefore:
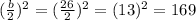
2. Complete the square by adding 169 to the expression given:
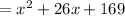
3. Factor it in order to express it as a binomial.
The answer is: