Question

What’s the steps to solve this?Answer options: square root of 40, square root of 50, 18 square units, 20 square units

Answer 1

The distance (d) between two points (x₁, y₁) and (x₂, y₂) is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

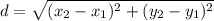
To find the area of the rectangle, find the distance between the points (sides of the rectangle.

Step 01: Finding the distance between A(-3, 0) and B(3,2).

`\begin{gathered} d_(AB)=√((3-(-3))^2+(2-0)^2) \\ d_(AB)=√(6^2+2^2) \\ d_(AB)=√(36+4) \\ d_(AB)=√(40) \end{gathered}`

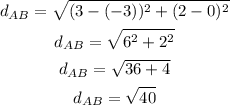
Step 02: Finding the distance between B(3,2) and C(4, -1).

`\begin{gathered} d_(AB)=√(()^2+()^2) \\ d_(AB)=√((4-3)^2+(-1-2)^2) \\ d_(AB)=√(1^2+(-3)^2) \\ d_(AB)=√(1+9) \\ d_(AB)=√(10) \end{gathered}`

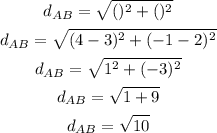
Step 03: Find the area of the rectangle.

The area (A) of the rectangle is length * width.

Then,

`\begin{gathered} A=√(40)*√(10) \\ A=√(400) \\ A=20square\text{ }units \end{gathered}`

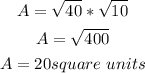
Answer: 20 square units.