Question

You deposit $ 142 each year into an IRA earning 4.6 % interest compounded annually. How much will you have in the account in 18 years?

Answer 1

We have to calculate the future value (FV) after n = 18 years of an investment of $142 each year, with a rate of interest of 4.6% (r = 0.046) compounded annually.

We can calculate the future value of an annuity like this as:

`FV=P\cdot((1+r)^n-1)/(i)`

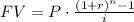
Replacing and calculating, we get:

`\begin{gathered} FV=142\cdot((1+0.046)^(18)-1)/(0.046) \\ FV=142\cdot(1.046^(18)-1)/(0.046) \\ FV\approx142\cdot(2.24683-1)/(0.046) \\ FV\approx142\cdot(1.24683)/(0.046) \\ FV\approx142\cdot27.1 \\ FV\approx3848.91 \end{gathered}`

Answer: She will have $3848.91 in her account.