Part A.
In order to see if R is a right angle, we need to find the slope of the line segments GR and RT.
The points G and R are
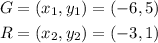
By substituting these point into the slope formula ,we have
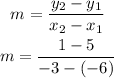
which gives
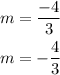
Now, lets find the slope of the line segment RT.
The points R and T are
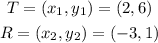
then, the slope is
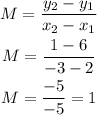
Finally, two lines segments are perpendicular (or in other words, R is a right angle) if one of the slopes is a negative reciprocal of the other, that is, the following equality must be fulfilled:
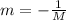
However, in our case, we can see that
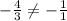
Therefore, R is not a right angle.
Part B.
We want to see if angle R is a right angle but with a new T, which is now T'. In this case, we can apply the same procedure but with the point T' as
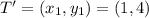
because T was (2,6) then T'=(2-1,6-2)=(1,4).
So, the new slope for the segment RT' is
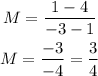
But now, we can see that
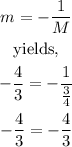
since both number are the same, then m is the negative reciprocal of the new M, therefore, the line segments GR and RT' are perpendicular, which implies that R is a right angle.