Given:
The function
![f(x)=x^3-3x^2+9x+5,\text{ on interval}[0,1]](https://img.qammunity.org/2023/formulas/mathematics/college/8ooyhkqdpyrppyo8j9opa7v8osk4x4adwt.png)
Required:
Determine whether the Mean Value Theorem can be applied to f on the closed interval [a,b]. If the Mean Value Theorem can be applied, find all values of in the open interval.
Step-by-step explanation:
![\begin{gathered} \text{ The mean value theorem states that for a continuous and differentiable} \\ \text{ function }f(x)\text{ on the interval }[a,b]\text{ there exists such number }c\text{ from the} \\ \text{ interval }(a,b),\text{ that }f^(\prime)(c)=(f(b)-f(a))/(b-a). \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/46vi91kdbsvqzeabch3gnj9f2pglh2fga7.png)
First evaluate the function at the endpoints of the interval:
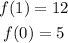
Next, find the derivative:
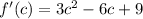
From the equation:
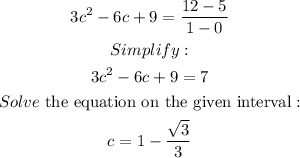
Answer:
Completed the answer.