Question

For f(x) = sqrt(x) and g(x) = x - 3 , find the following functions. I need help with C,D

Answer 1

Given the function f(x) and g(x) expressed as

`\begin{gathered} f(x)=√(x) \\ g(x)=x-3 \end{gathered}`

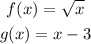
C)

`(f\circ g)(7)`

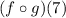
To evaluate,

step 1: Determine the function (f o g)(x).

The (f o g)(x) can be expressed as

`f(g(x))`

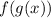
This implies that the g(x) function is substituted into the f(x) function.

Thus,

`\begin{gathered} (f\circ g)(x)=f(g(x))=f(x-3) \\ \Rightarrow(f\circ g)(x)=√((x-3)) \end{gathered}`

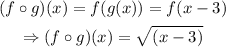
step 2: Evaluate (f o g)(7).

This is evaluated by substituting the value of 7 for x into the (f o g)(x) function.

Thus,

`\begin{gathered} \begin{equation*} (f\circ g)(x)=√((x-3)) \end{equation*} \\ \Rightarrow(f\circ g)(7)=√((7-3)) \\ =√(4) \\ \Rightarrow(f\circ g)(7)=2 \end{gathered}`

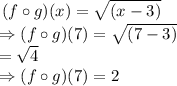
Hence, the value of the function (f o g)(7) is 2.

D)

`(g\circ f)(7)`

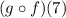
To evaluate,

step 1: Determine the function (g o f)(x).

The function (g o f)(x) can be expressed as

`g(f(x))`

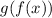
This implies that the f(x) function is substituted into the g(x) function.

Thus,

`\begin{gathered} (g\circ f)(x)=g(f(x))=g(√(x)) \\ \Rightarrow(g\circ f)(x)=√(x)\text{ -3} \end{gathered}`

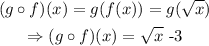
step 2: Evaluate (g o f)(7).

This is evaluated by substituting the value of 7 for x into the (g o f)(x) function.

Thus,

`\begin{gathered} \begin{equation*} (g\circ f)(x)=√(x)\text{ -3} \end{equation*} \\ \Rightarrow(g\circ f)(7)=√(7)\text{ -3} \end{gathered}`

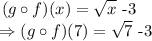
Hence, the value of the function (g o f)(7) is (√7 - 3).