1 Answer

FHannes · Answer 1 · 2024-01-02T12:10:47+0000

Hello!

First of all, let's divide the sentences contained in the exercise.

• Victor is 18.

Okay, this information is clear.

• Lolly is 3 times younger than Victor.

We can represent it as:

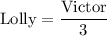
$\mathrm{Lolly=(Victor)/(3)}$

As we know the age of Victor, we can replace it and solve:

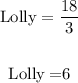
$\begin{gathered} \mathrm{Lolly=(18)/(3)} \\ \\ \mathrm{Lolly=}6 \end{gathered}$

• Holly is 6 times older than Lolly.

In the same way, we can represent it as:

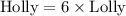
$\mathrm{Holly=6}*\mathrm{Lolly}$

As now we know that Lolly has 6 years, we can replace it too:

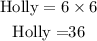
$\begin{gathered} \mathrm{Holly=6}*6 \\ \mathrm{Holly=}36 \end{gathered}$

Answers:

Victor: 18 years

Lolly: 6 years

Holly: 36 years