Question

The tree diagram shows the sample space of two-digit numbers that can be created using the digits 2, 1, 3, and 6. What is the probability of choosing a number from the sample space that contains 1 or 6 ?

Answer 1

If we look at the tree diagram, we can see that we have 12 numbers, they are:

{12, 13, 16, 21, 23, 26, 31, 32, 36, 61, 62, 63}

That's our sample space, if we look at each tree we can count how many numbers has 1 or 6, on the first tree we have 2 numbers: 21 and 26. On the second tree we have three numbers: 12, 13 and 16, that's expected because the first digit is 1. For the second tree we have just two, 31 and 36. For the last tree we have three again because of the digit 6.

Therefore the probability will be how many numbers that has 1 or 6 divided by the sample space, then

`\begin{gathered} P=(2+3+2+3)/(12) \\ \\ P=(10)/(12) \\ \\ P=(5)/(6) \end{gathered}`

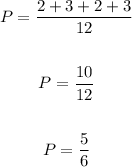
The probability is

`P=(5)/(6)`