Question

The figure on the right shows an 80N body sliding from rest on a rough inclined plane with an acceleration of 2m/s². If the plane is inclined to the horizontal plane at an angle of 30°, answer the following:Question one: draw a free body diagram for this body.Question two: calculate the coefficient of friction.Question three: calculate the force of friction.

Answer 1

Coefficient of friction: 0.34

Force of friction: 23.67 N

Step-by-step explanation:

The free-body diagram of the body is given below.

From the above diagram, we find that

`f_{\text{net}}=f_g-f_s_{}_{}_{}`

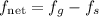
where fg is the force due to gravity and fs is the force due to friction.

Now

`f_g=mg\sin 30^o`

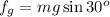
and

`f_s=\mu_sN=\mu_smg\cos 30`

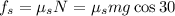
Therefore, we have

`f_{\text{net}}=mg\sin 30^o-\mu_smg\cos 30^o`
`\Rightarrow f_{\text{net}}=mg(\sin 30^o-\mu_s\cos 30^o)`

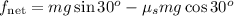
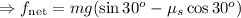
Newtons second law gives fnet = ma; therefore we have

`ma=mg(\sin 30^o-\mu_s\cos 30^o)`

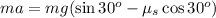
cancelling m from both sides gives

`a=g(\sin 30^o-\mu_s\cos 30^o)`

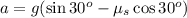
Now in our case a = 2.0 m /s^2 and g = 9.8 m /s^2 therefore,

`2.0=9.8(\sin 30^o-\mu_s\cos 30^o)`

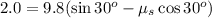
evaluating sin 30 and cos 30 gives

`2.0=9.8(0.5-\frac{\mu_s\sqrt[]{3}}{2})`

solving for μ gives

`\mu_s=\frac{2}{\sqrt[]{3}}(0.5-(2.0)/(9.8))`
`\boxed{\mu_s=0.34}`

Now we find the force of friction from the following:

`f_s=\mu_smg\sin 30`

We know that the weight of the object is 80N, meaning mg = 80, and therefore, the above equation gives

`f_s=0.34\cdot80\cdot\cos 30`
`\boxed{f_s=23.67N}`

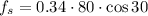
which is our answer!

Hence, to summerise:

Coefficient of friction: 0.34

Force of friction: 23.67 N