Question

Dakota puts 400.00 into an account to use for school expenses the account earns 13%interest compounded monthly how much will be in the account after 6 years

Answer 1

Let's first make a list of what is given in the scenario:

a.) Dakota puts 400.00 into an account to use for school expenses.

Principal Amount = 400

b.) The account earns 13% interest.

Interest rate = 13%

c.) It is compounded monthly.

n = 12

What is asked: How much will be in the account after 6 years? t = 6 years

For this type of situation, let's use the Compound Interest Formula:

`\text{ A = P(}1\text{ + }(r)/(n))^(nt)`

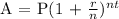
Where,

A = amount after being compounded a certain interest rate in a given time.

r = interest rate, in decimal form = 13% = 13%/100% = 0.13

n = number of times the interest is being compounded = 12

t = time = 6 years

P = Principal/Initial Amount = 400.00

Let's plug in the values in the formula to be able to determine how much will be in the account after 6 years:

`\text{ A = P(}1\text{ + }(r)/(n))^(nt)\text{ }\rightarrow\text{ A = (400)(}1\text{ + }\frac{\frac{13(\text{\%)}}{100(\text{\%)}}}{12})^((12)(6))`
`\text{ A = (400)(1 + }(0.13)/(12))^(72)=(400)(1+0.010833)^(72)=(400)(1.010833)^(72)`
`\text{ A = (400)(2.1722891629)}`
`\text{ A = 868.915665 }\cong\text{ 868.92}`

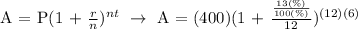
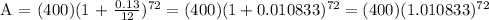
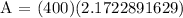
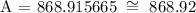
Therefore, Dakota's account will become 868.92 in 6 years at 13% interest compounded monthly.