Step-by-step explanation:
We can find the equation of a line using the following:

Where m is the slope and (x1, y1) are the coordinates of a point.
Now, we can replace (x1, y1) by (-3, 6) and m by 4/(-5) to get:
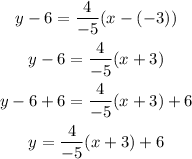
Now, we can replace the value of x, to find another point in the graph.
So if x = 2 then:
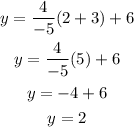
Answer:
Therefore, the lines pass through the points (-3, 6) and (2, 2) and the graph of the line is: