Question

A street light is at the top of a 19 foot tall pole. A woman 5.25 feet tall walks towards the pole with a speed of 7ft/sec along a straight path. How fast is the tip of her shadow moving when she is 35ft from the base of the pole?

Answer 1

Answer:

The tip of her shadow is moving at the speed of 9.66 ft/sec

Step-by-step explanation:

The height of the street light = 19 feet

The height of the woman = 5.25 feet

Distance between the woman and the base of the pole, x = 35 ft

The speed of the woman towards the pole, dx/dt = 7ft/sec

The distance from the base of the streetlight to the tip of the woman's shadow = y

The distance from the woman to the tip of her shadow = y - x

The diagram illustrating this description is shown below

Using similar triangle:

`\begin{gathered} (19)/(5.25)=\text{ }(y)/(y-x) \\ 19(y-x)\text{ = 5.25y} \\ 19y-19x\text{ = 5.25y} \\ 19y-5.25y\text{ = 19x} \\ 13.75y\text{ = 19x} \\ y\text{ = }(19)/(13.75)x \\ y\text{ = }1.38x \end{gathered}`

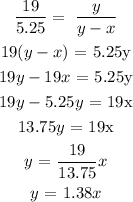
Find the derivative of both sides with respect to time, t

`\begin{gathered} (dy)/(dt)=\text{ 1.38}(dx)/(dt) \\ (dy)/(dt)=\text{ 1.38(7)} \\ (dy)/(dt)\text{ = }9.66\text{ ft/sec} \end{gathered}`

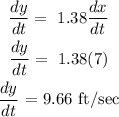
The tip of her shadow is moving at the speed of 9.66 ft/sec