Question

Answer the question with steps.. and solve the equation using quadratic formula.!

Answer 1

Given the equation

`(6x^2-7x+2)(x^2-5x+5)\text{ = 0}`

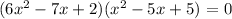
The equations in bracket are both quadratic equations, hence we are going to equate both to zero and factorize as shown;

`\begin{gathered} 6x^2-7x+2=0 \\ x^2-5x+5\text{ =0} \end{gathered}`

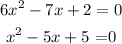
Factorize both equations;

For 6x^2-7x+2 = 0

6x^2-3x-4x+2 = 0

3x(2x-1)-2(2x-1) = 0

(3x-2)(2x-1) = 0

3x-2 = 0 and 2x-1 = 0

3x = 2 and 2x = 1

x = 2/3 and x = 1/2

Also for the second equation;

x^2-5x+5 = 0

Using the general formula;

`\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(1)(5)}}{2} \\ x\text{ =}\frac{5\pm\sqrt[]{25^{}-20}}{2} \\ x\text{ = }\frac{5\pm\sqrt[]{5}}{2} \\ x\text{ = }(5+2.24)/(2)\text{ and }(5-2.24)/(2) \\ x=(7.24)/(2)\text{ and }(2.74)/(2) \\ x\text{ = 3.62 and 1}.37 \end{gathered}`

Hence the values of x are 2/3, 1/2, 3.62 and 1.37