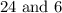Question

A.

The sum of two numbers is thirty. One number is five times the other less six. Find thenumbers.

Answer 1

Let be "x" and "y" the numbers you must find.

You need to remember that:

- A Sum is the result of an Addition.

- "Times" indicates a Multiplication.

- "Less" indicates a Subtraction.

Then, "The sum of two numbers is thirty" can be represented with the following equation:

`x+y=30`

And "One number is five times the other less six" can be represented with the following equation:

`x=5y-6`

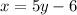
Now you can set up the following System of Equations:

`\begin{cases}x+y=30 \\ x=5y-6\end{cases}`

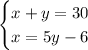
You can solve it by applying the Substitution Method:

1. Substitute the second equation into the first one.

2. Solve for "y".

Then:

`\begin{gathered} (5y-6)+y=30 \\ 6y-6=30 \\ 6y=30+6 \\ \\ y=(36)/(6) \\ \\ y=6 \end{gathered}`

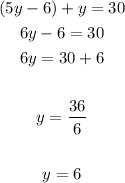
3. Substitute the value of "y" into the second equation and evaluate, in order to find the value of "x":

`\begin{gathered} x=5y-6 \\ x=(5)(6)-6 \\ x=30-6 \\ x=24 \end{gathered}`

Therefore, the answer is:

`\begin{gathered} 24\text{ and }6 \\ \end{gathered}`