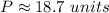Question

Line AB with endpoints A(4,4) and B(5,-1) is reflected in the line y=x to create its image Line A’B’. Graph A’B’. Then, find the perimeter of the figure formed by the segments Line AB , Line B’B and Line AB’ to the nearest tenth. The grey line was already graphed for me already. I started by graphing the points 4,4 and 5,-1. Then I reflected it in the line y=x but I’m having trouble figuring out the perimeter.

Answer 1

• Given the line AB whose endpoints are:

`\begin{gathered} A\mleft(4,4\mright) \\ B\mleft(5,-1\mright) \end{gathered}`

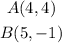
You know that the line of reflection is:

`y=x`

By definition, the rule for that Reflection is:

`(x,y)\rightarrow\mleft(y,x\mright)`

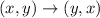
Then, the endpoints of the Image A'B' are:

`\begin{gathered} A(4,4)\rightarrow A^(\prime)(4,4) \\ B(5,-1)\rightarrow B^(\prime)(-1,5) \end{gathered}`

Therefore, you can notice that the lines of AB and A'B' are graphed correctly.

• According to the information given in the exercise, you must find the perimeter of the figure formed by these segments:

`\begin{gathered} AB \\ B^(\prime)B \\ AB^(\prime) \end{gathered}`

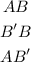
Look at the following picture, where you can see the segments that form a triangle:

You can see in the picture a triangle that is formed by the segments AB, B’B and AB'.

To find the length of each segment by using the formula for calculating the distance between two points:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Where the points are:

`(x_1,y_1);(x_2,y_2)_{}`

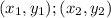
Therefore, knowing the endpoints of each segment of the triangle, you get:

- Length of the side AB:

`AB=\sqrt[]{(5-4)^2+(-1-4)^2}`
`\begin{gathered} AB=\sqrt[]{(1)^2+(-5)^2} \\ AB=\sqrt[]{26} \end{gathered}`

- Length of the side AB':

`A^{}B^(\prime)=\sqrt[]{(-1-4)^2+(5-4)^2}=\sqrt[]{26}`

- Length of the side B'B:

`B^(\prime)B=\sqrt[]{(-1-5)^2+(5-(-1))^2}=6\sqrt[]{2}`

Knowing the length of each side, you can add them in order to find the perimeter:

`P=\sqrt[]{26}+\sqrt[]{26}+6\sqrt[]{2}\approx18.7\text{ }units`

Therefore, the answer is:

`P\approx18.7\text{ }units`