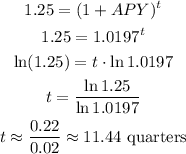Question

Logarithm 3) Abe deposits $1500 into a savings account that pays 1.96% per year compounded quarterlyfor + years.a) What is the APy for this compound interest model?b) How long before the amount in the account reaches $2000?

Answer 1

The initial deposit is $1500, the annual rate is 1.96%, compounded quarterly.

For a given annual rate r and n compounded periods, the APY is given by:

`\text{APY}=(1+(r)/(n))^n-1`

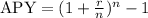
a) For r = 0.0196 and n = 4, we have:

`\begin{gathered} \text{APY}=(1+(0.0196)/(4))^4-1_{} \\ \text{APY}=1.0049^4-1 \\ \text{APY}=1.0197-1 \\ \text{APY}=0.0197=1.97\% \end{gathered}`

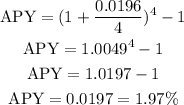
b) $2000 represent an increase of 25% in relation to $1500. In this case, we have:

`\begin{gathered} 1.25=(1+APY)^t \\ 1.25=1.0197^t \\ \ln (1.25)=t\cdot\ln 1.0197 \\ t=(\ln 1.25)/(\ln 1.0197) \\ t\approx(0.22)/(0.02)\approx11.44\text{ quarters} \end{gathered}`