Given
The ratios,
A. 1 : 6 and 3 : 18
B. 2 : 14 and 3 : 42
C. 12 : 6 and 2 : 1
D. 3 : 11 and 6 : 22
To find the ratios which are not equal.
Step-by-step explanation:
It is given that,
A. 1 : 6 and 3 : 18
That implies,
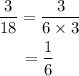
Hence, the ratios 1 : 6 and 3 : 18 are equal.
B. 2 : 14 and 3 : 42
That implies,
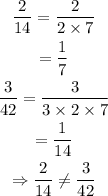
Hence, the ratios 2 : 14 and 3 : 42 are not equal.
C. 12 : 6 and 2 : 1
That implies,
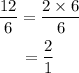
Hence, the ratios C. 12 : 6 and 2 : 1 are equal.
D. 3 : 11 and 6 : 22
That implies,
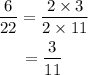
Hence, the ratios D. 3 : 11 and 6 : 22 are equal.
Thus, the ratios B. 2 : 14 and 3 : 42 are not equal.