Question

At the pool, Janae jumps off a diving board that is 15 feet high. Janaes height above the water is modeled by the function f(x)=-5x^2+10x+15. A: Janae wants to know how high she jumped in the air before diving towards the water. If she drew the path of her diving on a graph, what is the name of the mathematical point on the parabola she would need to find?

Answer 1

To obtain the maximum value that she will jump, we will

1. Differentiate the given function

2. Equate it to 0, and obtain a value for x

3. Substitute the value of x back into the intial function and obtain what f(x) will be. The value that we obtain will be the maximum value.

Step 1:

`\begin{gathered} f(x)=-5x^2+10x+15 \\ (df)/(dx)=2(-5)x^(2-1)+1(10)x^(1-1)+0 \\ =-10x^1+10x^0 \\ =-10x+10 \end{gathered}`

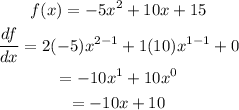
Step 2:

`\begin{gathered} (df)/(dx)=0 \\ -10x+10=0 \\ -10x=-10 \\ x=(-10)/(-10) \\ x=1 \end{gathered}`

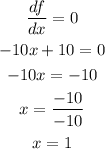
Step3:

`\begin{gathered} f(x)=-5x^2+10x+15 \\ substitutIng\text{ x=1 into f(x), we will obtain the maximum value} \\ f(1)=-5(1)^2+10(1)+15 \\ f(1)=-5+10+15 \\ f(1)=20 \end{gathered}`

Therefore the highest(maximum) point that Jane will reach in the air is 20feet.