Question

I need help with this tutor please and thank you

Answer 1

for this

we will calculate the slopes

for AB line point A is (3, -1) and B (2, -4)

so the slope is

`m=(-4-(-1))/(2-(3))=(-3)/(-1)=3`

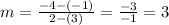
for line A'B' the point A' is (-1, -3) and B' is (-4, - 2)

so the slope i s

`m=(-2-(-3))/(-4-(-1))=(1)/(-3)`

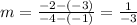
multiply both slope

`=(1)/(-3)*3=-1`

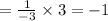
the product of both the slope is -1

so they are at 90 degrees or perpendicular to each other,

so the answer is option A.