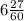Gavin had 20 minutes to do a three-problem quiz.
He spent 9 3/4 minutes on problem 1.
He spent 3 4/5 minutes on problem 2.
How much time did he have left for problem 3?
We need to add the time spent on problem 1 and problem 2 and then subtract the sum from the total time.
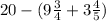
Simplify the above fraction
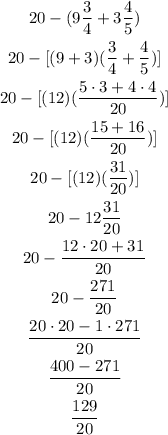
Let us write the answer in mixed number
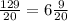
Finally, convert the fractional part to seconds by multiplying the fractional part by 3
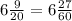
This means that there are 6 minutes and 27 seconds are left for problem 3.