Question

The Haber-Bosch process is a very important industrial process. In the Haber-Bosch process, hydrogen gas reacts with nitrogen gas to produce ammonia according to the equation3H2(g)+N2(g)→2NH3(g)The ammonia produced in the Haber-Bosch process has a wide range of uses, from fertilizer to pharmaceuticals. However, the production of ammonia is difficult, resulting in lower yields than those predicted from the chemical equation.1.48 g H2 is allowed to react with 9.97 g N2 , producing 1.81 g NH3 .What is the theoretical yield in grams for this reaction under the given conditions?What is the percent yield for this reaction under the given conditions?Express your answer to three significant figures and include the appropriate units.

Answer 1

Answer;

Theoretical yield = 8.33 grams

percent yield = 21.7%

Explanations:

Given the balanced chemical reaction between hydrogen and nitrogen to produce ammonia expressed as:

`3H_2(g)+N_2(g)\rightarrow2NH_3(g)`

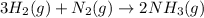
Given the following parameters

Mass of H2 = 1.48grams

Mass of N2 = 9.97grams

Determine the moles of each reactant

`\begin{gathered} moles\text{ of H}_2=\frac{mass}{molar\text{ mass}} \\ moles\text{ of H}_2=(1.48g)/(2.016gmol^(-1)) \\ moles\text{ of H}_2=0.734moles \\ moles\text{ of 1 atom }of\text{ H}_2=(0.734)/(3)=0.245moles \end{gathered}`
`\begin{gathered} moles\text{ of N}_2=(9.97)/(28) \\ moles\text{ of N}_2=0.356moles \end{gathered}`

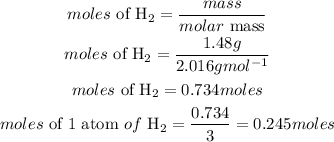
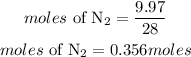
Since the moles of 1 atom of H2 gas is lower than that of nitrogen gas, hence H2 is the limiting reactant

According to stoichiometry, 3 moles of H2 produces 2 moles of ammonia, the moles of ammonia required will be:

`\begin{gathered} moles\text{ of NH}_3=(2)/(3)*0.734 \\ moles\text{ of NH}_3=0.489moles \end{gathered}`

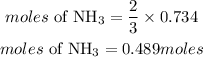
Determine the mass of NH3 (theoretical yield)

`\begin{gathered} Mass\text{ of NH}_3=moles* molar\text{ mass} \\ Mass\text{ of NH}_3=0.489moles*(17.031g)/(mol) \\ Mass\text{ of NH}_3=8.33grams \end{gathered}`

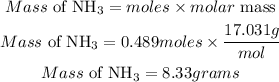
Hence the theoretical yield in grams for this reaction is 8.33 grams

Determine the percentage yield

`\begin{gathered} \%yield=(actual)/(theoretical)*100 \\ \%yield=(1.81g)/(8.33g)*100 \\ \%yield=0.217*100 \\ \%yield=21.7\% \\ \end{gathered}`

Therefore the percent yield for this reaction is 21.7%