Question

If you invest $10,427.00 into ancaring an annual nominal interest rate of 4.502%, how much will you have in your account after 11 years if the interest is compounded quarterly? If the interest is compounded continuously?Help solve B If interest is compounded continuously: FV= ___

Answer 1

The continuous compounding formula is given to be:

`A=Pe^(rt)`

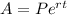
where

P = the initial amount

A = the final amount

r = the rate of interest

t = time

e is a mathematical constant where e ≈ 2.7183.

From the question, we have the following parameters:

`\begin{gathered} P=10,427 \\ r=(4.502)/(100)=0.04502 \\ t=11 \end{gathered}`

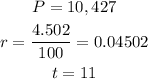
Inputting these values into the formula, we have:

`\begin{gathered} A=10427e^(0.04502*11) \\ A=$17,109.24$ \end{gathered}`

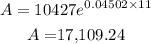
Therefore, the final value when compounded continuously is $17,109.24.