Question

Solve the inequality for x and identify the graph of its solution. x + 3< 2 Choose the answer that gives both the correct solution and the correct graph. A Solution: xs-5 or x>-1 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 2 B. Solution: x< 1 or x> 5 -2 -1 0 1 2 3 4 5 6 7 8 C. Solution: x> -5 and x < -1 --8-7 -6 -5 -4 -3 -2 -1 0 1 1 2 D. Solution: x>-5 and x < -1 OD -8 -7 -6 -7 -6 -5 44 3 -2 0 1 다. 2

Answer 1

We must solve the following inequality:

`|x+3|<2`

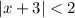
In order to solve the problem we consider the two cases:

1) When the expression inside the absolute value fuction is positive we obtain:

`\begin{gathered} x+3<2 \\ x<2-3 \\ x<-1 \end{gathered}`

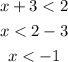
2) When the expression inside the absolute value fuction is negative we obtain:

`\begin{gathered} -(x+3)<2 \\ x+3>-2 \\ x>-2-3 \\ x>-5 \end{gathered}`

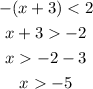
So we have the following conditions:

`x>-5\text{ and x <-}1`

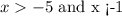
The correct answer is letter C.